Topics
- Data modeling
- Linear regression
- Regularization
- Logistic regression
- Support Vector Machine (SVM)
- Random Forest
Data Modeling
feature(x or input) 와 label(y or output)를 효과적으로 설명하는 함수를 만드는 일
- label 존재 여부에 따른 분류
| label 존재하는 경우 | label 존재하지 않는 경우 |
| supervised learning | unsupervised learning |
- label 데이터 종류에 따른 분류
| continuous data | categorical data |
| regression task | classification task |
Bayes 정리를 Data modeling 관점에서 이를 바라볼 때,
P(θ | X) = P(X | θ) P(θ) / P(X) 로 표현 가능하다. (X : 관측된 데이터, θ : 데이터에 대한 가설, 즉 Parameter value)
Bayes Theorem explanation
https://corporatefinanceinstitute.com/resources/data-science/bayes-theorem/
Bayes' Theorem
The Bayes theorem (also known as the Bayes’ rule) is a mathematical formula used to determine the conditional probability of events.
corporatefinanceinstitute.com
궁극적인 목적은 P(θ|X) 를 최대화하는 θ를 찾는 것이다. P(θ) 가 일정하다는 가정에서는 P(X|θ)를 최대화하는 θ를 MLE 하고, P(X)가 일정하다는 가정에서는 P(X|θ)P(θ) 를 최대화하는 θ를 MAP 하는 과정을 Data modeling 이라고 할 수 있다.
Data Modeling 과정
- 데이터 전처리 및 분석
- 데이터를 Training set과 Test set으로 분류
- Training set에 대해 사용할 model을 학습 (model.fit(training_set))
- Test set에 대해서 학습된 모델의 예측값을 통해 모델의 성능 평가 (실제값 vs 예측값)
- 만일 모델의 성능이 쓸만하다고 판단될 경우, 새로운 데이터에 대해 학습된 모델을 이용하여 label 값 예측 (inference 과정)
from sklearn.datasets import make_regression
X, y = make_regression(n_samples = 100, n_features = 5, noise = 50, random_state = 42)
from sklearn.model_selection import train_set_split
X_train, X_test, y_train, y_test = train_set_split(X, y, random_state = 33)
lr = LinearRegression(normalize = True)
lr.fit(X_train, y_train)
y_pred = lr.predict(X_test)
print(mean_squared_error(y_test, y_pred))
y_infer = lr.predict(X_infer)
Linear regression
x와 y 간의 "선형 관계" 가 있다고 가정할 때 사용한다.
- Simple Linear Regression
한 개의 독립 변수 x와 한 개의 종속 변수 y를 표현
y = b + wx ( b : bias, w : weight)
weight와 bias, Activation function 의 설명을 간략하게 하자면 아래와 같다.
Weight : 중요도를 다르게 한다.
Bias : 최종 출력 값을 조절한다. 즉, 임계점을 얼마나 쉽게 넘을지 말지 조절해주는 값.
Activation function : 값을 결정하는 0과 1의 경계선을 두고 의사를 결정하게 되는 함수.
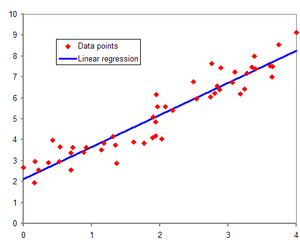
- Multiple Linear Regression

여러 개의 독립 변수와 하나의 종속 변수를 표현한다.
그렇다면, nonlinear regression을 linear regression 으로 바꾸려면, 어떻게 해야 할까?

Transformation, Scaling을 이용해서 Linear Regression 형태로 다시 만들 수 있다.
- Linear Regression 가정
1. Normality
E(ε) = 0, ε ~ N(0, σ^2)
Linear regression은 회귀 모형을 추정한 이후 모형과 잘 맞는지 모형 검정과 계수 검정을 필요로 한다. 이러한 가설 검정을 하기 위해서는 분포 가정이 필요한데, 이 때 정규성 가정을 사용한다.
2. Homoscendasticity
Var(ε) = σ^2 (일정한 분산을 가진다)
정규성과 마찬가지로 검정을 용이하게 만들기 위해 사용한다.
3. Independency
Cov(X, ε) = 0, Cov(εi, εj) = 0
오차항은 서로 독립이라고 가정하지 않으면, 즉 상관관계가 존재한다면 Linear regression으로 설명될 수 없는 다른 관계가 존재한다는 의미이므로 정확도를 떨어뜨림.
Cost Function
Loss function, Objective function 이라고도 불린다. 실제로는 3가지 정의가 약간 다르지만, 데이터 분야에서는 두루두루 사용된다. Cost function 은 실제값과 예측값의 오차에 대한 식이다. Linear regression 에서는 RSS, MSE를 Cost function 으로 사용한다.
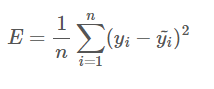
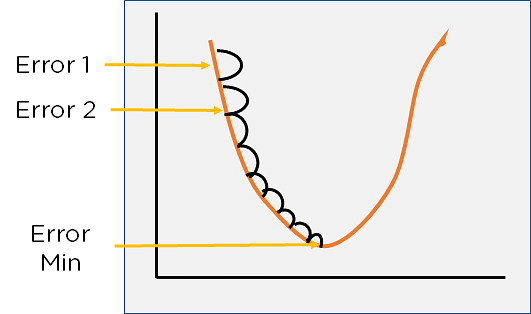
Cost function이 differentiable (미분가능) 하고 convex (아래로 볼록) 할 때, Min은 cost function을 w, b로 각각 편미분하였을 때 0이 되는 지점이다.
OLS (Ordinary Least Squares)
오차를 최소화하는 w, b를 추정하는 방법
제곱의 합을 최소로 만드는 점을 찾기 위해서는 고등학교에서 배운 f'(x) = 0, f''(x) > 0을 사용한다.
- f'(x) = 0
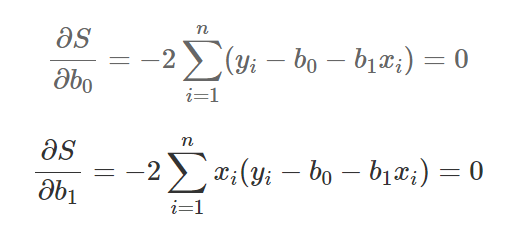
- 이차 편미분 행렬
"f'(x) = 0" 조건은 최소 또는 최대가 되는 점을 찾는 조건이기 때문에, 최소가 되는 점을 찾으려면 또 하나의 조건으로 이차 편미분 행렬이 양정치 행렬을 만족해야 한다.
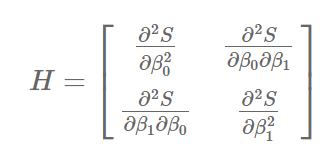

따라서, B0와 B1의 값은 아래와 같이 결론이 된다.
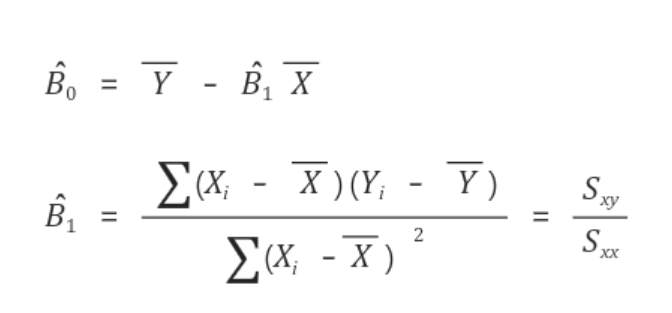
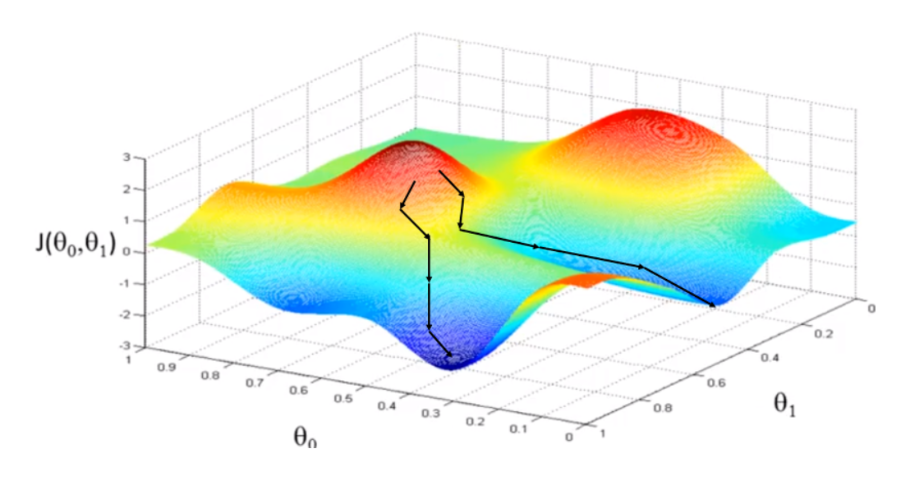
Gradient descent
변수가 많아지거나, cost function이 복잡해지는 경우 OLS 를 통해 loss 가 최소인 parameter 를 추정하는 것이 어렵다. 그래서 cost function 의 gradient value 를 learning rate 만큼 여러 번 update 하여 찾아가는 방식을 Gradient descent 라고 한다. 이 방법을 사용하는 경우는 보통 데이터가 많으므로 여러 단계에서 mini-batch 만큼 데이터를 sampling 하여 학습하는SGD(mini-batch Stochastic Gradient Descent) 방식을 사용한다.

Learning Rate (학습률)
인공 신경망 모델이 습을 진행할 때 각각의 가중치(weight)를 얼마나 업데이트할지 결정하는 Hyperparameter.
학습률이 너무 작으면 weight update 속도가 느려져서 학습 속도가 느려질 수 있다. 단지 작아도 weight update 가 미세하게 이루어져 local mininum 에 빠질 가능성이 있음. 반대로 크면 학습 중에 발산할 가능성이 존재한다. 따라서, 너무 작지도 크지도 않은 적당한 값을 지정하여야 한다.
Hyperparameter
parameter 와는 다른 값인 Hyperparameter 는 주로 알고리즘 사용자가 경험에 의해 직접 세팅하는 값이다.
parameter 는 모델 내부에서 결정되는 변수로, 측정되거나 학습을 통해 얻어진다.
Regularization
Regularization 을 설명하기 전, overfitting에 대하여 설명하겠다. Overfitting (과적합, high variance) 란 학습 데이터에 의해서 과하게 fitting 되는 경우를 말한다. 이것이 발생하는 경우 test set에서의 loss가 증가할 수 있기 때문에, 실제 inference model 에서 generalize 되기 어려워진다. Overfitting 은 데이터에 내재된 complexity 보다 model 의 complexity 가 더 과한 경우나 dataset size 가 작은 경우 자주 발생한다. Linear regression 의 경우 변수가 많아질수록 Overfitting 발생 가능성이 높아진다.
Overfiittng을 줄이기 위해서는 모델의 복잡도를 줄여 중요한 feature들만 모델의 input으로 사용하는 방법이다. 또 하나의 방법은 Regularization을 사용하는 방법이다.
Regularization 은 model 의 complexity 를 제한하는 방법으로 한마디로 정의하자면 weight 가 너무 큰 값을 가지지 않도록 하는 방법이라고 할 수 있다. weight 가 너무 큰 값을 가지게 되면 구불구불한 형태의 함수가 만들어지는데, 이것을 방지하기 위해 Regularization 을 사용한다. 결국, outlier 의 영향을 적게 받도록 하고 싶은 것이다.
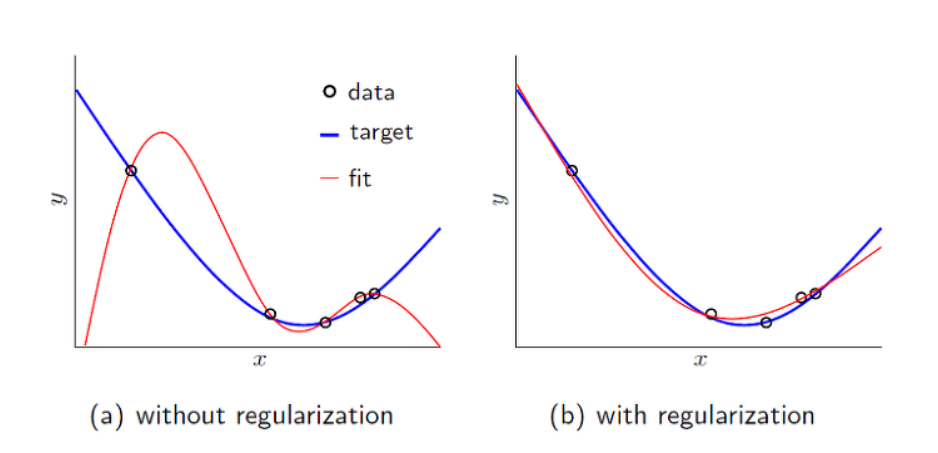
- L1 Regularization
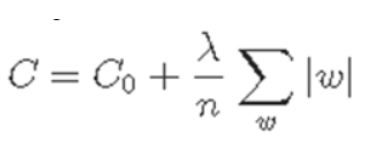
C0 : cost function, n : training data size, λ : regularization variable
w의 절대값을 추가하여 weight 의 부호에 따라 값을 바꾸는 형식으로 regularization 수행한다.
- L2 Regularization
L1 과는 다르게, 절대값 대신 squrare 를 사용하여 값을 바꾼다.

Ridge
최소제곱법과 유사하나, L2 loss를 추가하여 Regularization 한다.

더 높은 차원의 모델을 만들었을 때, 높은 차원을 낮은 차원으로 끌어내리는 제약을 건다. 즉, L2 loss를 이용하여 제약을 가해 그 제약 안에서 최소 error 를 발생하도록 하는 parameter를 Regularization 한다.

Lasso
L1 loss 를 이용하여 제약을 가하는 방법이다.
여기서는 L1 loss 에서 사용하는 weight 은 절대값이기 때문에, 마름모 모형으로 나온다. 하지만 이 방법은 Ridge 방법과는 다르게 미분이 불가능하다.
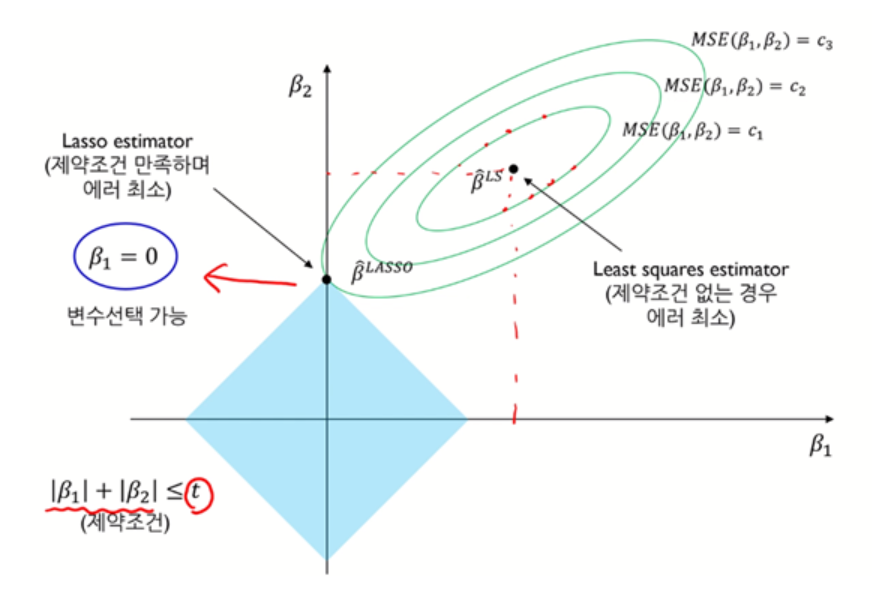
따라서, Regularization 은 λ 값을 조절하여 overfitting 을 방지한다.
Logistic Regression
classification task 에 적합한 Linear regression model.
Linear regression label value 에 "Sigmoid function" 을 적용하여 0과 1 사이의 값으로 만든다.
Sigmoid function 은 인공 뉴런의 activation function 으로 사용하거나, 정규 분포, t-분포에서도 사용된다.
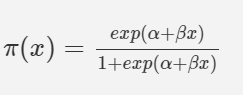
SVM (Support Vector Machine)
Linear regression 에서 허용 오차 안에 있는 오차값만 허용해주는 것.
오차값을 허용하는 것이 loss function algorithm 을 만든다. 허용 오차를 잘 설정하여야 좋은 성능을 가진 모델을 만들 수 있음.
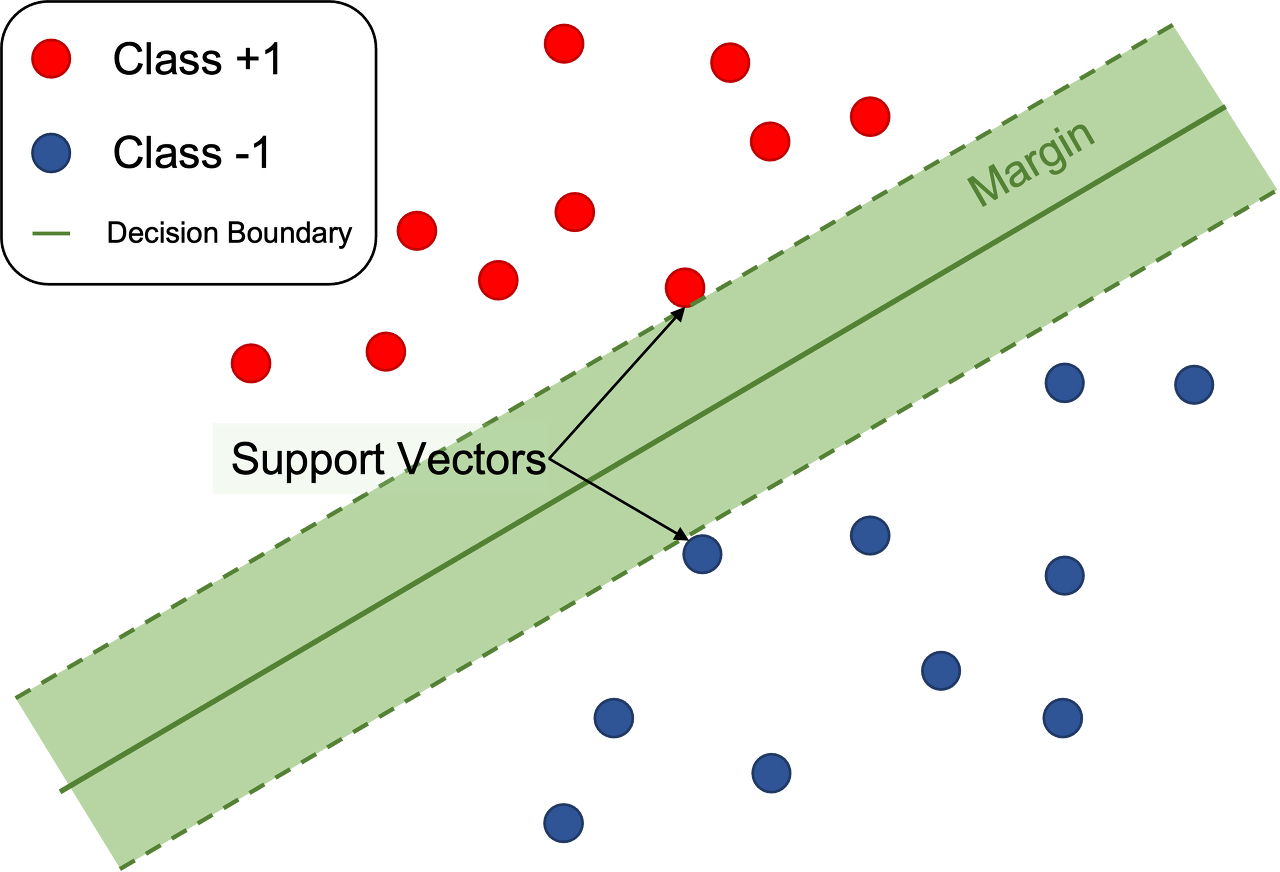
- kernal
설정을 통해 모델이 가정하는 x와 y의 관계를 잘 잡아낼 수 있음.
Random Forest
Random forest 란 여러 개의 Decision tree 를 만들어 그 결과들을 종합적으로 고려해서 결론을 도출하는 방법이다.
Decision tree를 random 으로 여러 개 만든 후에 각 tree 마다 나온 decision 을 voting 을 통하여 최종적인 label 값을 예측한다. 여기서 Decision Tree 란 특정 기준에 따라 데이터를 구분하는 모델이다. 한 번의 분기 때마다 변수 영역을 두 가지로 분류한다.


즉, 약한 여러 모델을 조합하여 더 정확한 예측을 해주는 방법이라고도 볼 수 있다.
- Random forest 특징
1. 분류(classification), 회귀(Regression)문제에 모두 사용 가능하다.
2. 결측치(Missing value)를 다루기 쉽다.
3. 대용량 데이터 처리가 쉽다.
4. 과적합(Overfitting) 문제를 해결해준다.
5. 특성중요도(Feature importance)를 구할 수 있다.
hyperparameter (여기서는 트리의 개수와 길이) 를 설정하여 모델의 성능을 높일 수 있지만, 무작정 많고 길다고 하여 성능이 좋아지진 않는다. (overfitting 이 이에 대한 원인 중 하나) 그리고 이렇게 되면 Memory 가 지나치게 커질 수 있어 효율성 문제 또한 존재한다.
'Bootcamp' 카테고리의 다른 글
| [Week 11] Day 2 - TIL (1) | 2024.02.06 |
|---|---|
| [Week 11] Day 1 - TIL (0) | 2024.02.05 |
| [Week 10] Day 1 - TIL (2) | 2024.02.05 |
| [Week 8] Day 1 - TIL (2) | 2024.01.08 |
| [Week 7] Day 1 - TIL (1) | 2024.01.06 |

